fevereiro « 2013 « It is Relative, I Think!

Tópicos Introdutórios de Mecânica Clássica – Parte 1, Parte 2, Parte 3.

Comentário Inicial

Esse é nosso ultimo post da seqüência de três posts sobre uma introdução a mecânica clássica para alunos do primeiro ano da graduação de física em engenharia. Nesse texto trataremos de três tópicos principais, primeiramente veremos campos, potencial e energia potencial, depois veremos o potencial de Lennard-Jones que é uma aplicação interessante do que vimos sobre energia potencial e para encerrar falaremos sobre teoremas de conservação do momento linear e angular, mas sem entrar em mérito da mecânica analítica.

O campo, o potencial e a energia potencial

Muito falamos sobre campos, principalmente o gravitacional e o elétrico.

Como sabemos a força elétrica entre duas cargas, $q_{1}$ e $q_{2}$ , é dada por

$\vec{F}=Kq_{1}q_{2}\frac{\vec{r}}{r^{3}}$

e a força gravitacional entre duas partículas com massas $m_{1}$ e $m_{2}$ , é;

$\vec{F}=-Gm_{1}m_{2}\frac{\vec{r}}{r^{3}}$

Como nosso objetivo é compreender o que é o campo, vamos analisar a força nesse conceito. Podemos dizer que a carga $q_{1}$ situada em um ponto $P$ produz uma “condição” em $R$ de tal forma que quando colocamos a carga $q_{2}$ em $R$ ela “sente” a força elétrica atuando sobre ela. Nesse caso chamaremos essa “condição” produzida por $q_{1}$ de $\vec{E}$ , assim $\vec{F}$ é a resposta de $q_{2}$ a $\vec{E}$ e podemos escrever a força como:

$\vec{F}=q_{2}\vec{E}$

Em que $\vec{E}$ é o vetor campo elétrico que é dado por

$\vec{E}=kq_{1}\frac{\vec{r}}{r^{3}}$

É importante notar que podemos (e devemos!) ver essa situação sobre dois aspectos, o primeiro é que esse campo em questão é produzido por algo que pode ser uma carga ou uma massa, o segundo é que esse campo atua em algo (carga ou massa). Essa simples analise não deve ser subestimada, uma vez que a realidade pode ser bem complexa.

Para o caso gravitacional podemos fazer exatamente a mesma coisa, tanto que na descrição acima já generalizei tanto para campos criados por cargas quanto por massas. Sendo assim, para a força gravitacional, temos;

$\vec{F}=-Gm_{1}m_{2}\frac{\vec{r}}{r^{3}}$

então

$\vec{F}=m_{2}\vec{C}$

Em que $\vec{C}$ é o campo gravitacional produzido por $m_{1}$ , em que $\vec{C}= Gm_{1}\frac{\hat{r}}{r^{3}}$ que, assim como o campo elétrico, possui direção radial. O $\vec{C}$ possui três componentes sendo cada uma delas uma função de $\left(x,y,z\right)$ , assim qualquer objeto que crie um campo estará criando um vetor $\vec{C}$ .

A energia potencial é energia propriamente dita e está relacionada a um sistema de interação entre dois ou mais corpos. Podemos defini-la em termos da força gravitacional, uma vez que ela é conservativa:

$U=-\int \vec{F} \cdot d\vec{s}=-m_{2}\int \vec{C} \cdot d\vec{s}= \frac{Gm_{1}m_{2}}{r_{1,2}}$

Podemos ver que no caso gravitacional temos a energia associada à interação entre as massas por meio do campo gravitacional criado por elas. O mesmo vale para o caso eletrostático, porém o campo é gerado por cargas elétricas.

Agora vamos nos atentar para uma coisa específica, a integral $\int \vec{C} \cdot d\vec{s}$ é o que chamamos de potencial, e podemos escrevê-lo da seguinte forma:

$V=\frac{U}{m_{2}}=\int \vec{C} \cdot d\vec{s}=-G\frac{m_{1}}{r}$

Porém a energia e o potencial só podem ser calculados em relação a algum ponto, e obtemos apenas sua variação, mas muitas vezes escolhe convenientemente regiões onde o potencial inicial ou a energia inicial é zero, para desconsiderar constantes aditivas.

É evidente que uma variação na energia potencial é igual a menos o trabalho, como falamos anteriormente, $\Delta U=-W$ , assim o potencial $V$ pode ser escrito como:

$V(r)=-\frac{W}{m_{2}}$

Assim o potencial pode ser entendido como o trabalho para deslocar uma massa unitária de um ponto a outro do campo. Considerando que nenhum desses pontos esteja infinito, mas sim em $A$ e $B$ , temos:

$V_{A}-V_{B}=\frac{W_{AB}}{m}$

Assim vemos que podemos traduzir a definição do potencial citada acima como o potencial sendo o trabalho por unidade de massa, no caso do campo gravitacional. No caso do campo elétrico o potencial é o trabalho por unidade de carga.

Uma outra forma, essa bem simples, de se entender o potencial é pensar que você está segurando uma bola a uma determinada altura do chão, quanto mais alto você levantar a bola em relação ao chão, maior o seu “potencial” de conseguir atingir o chão com uma determinada energia pra uma mesma massa, ou seja, esse potencial independe da massa da bola, já a energia propriamente dita vai depender da massa dessa bola.

A ultima coisa interessante sobre o potencial (para esse texto) é a sua relação direta com o campo. Uma vez que a variação da energia potencial é;

$\Delta U=W_{A \rightarrow B}=\int_{a}^{b}\vec{F}\cdot d\vec{s}=m_{2}\int_{a}^{b}\vec{C}\cdot d\vec{s}$

Então para o potencial temos:

$V_{a}-V{b}=\int_{a}^{b}\vec{C}\cdot d\vec{s}$

Assim para temos a seguinte relação entre o campo elétrico e o potencial:

$\vec{C}=-\nabla V$

Ou seja, o campo é igual ao negativo do gradiente de um potencial escalar. Isso nos mostra que em regiões onde o potencial é constante o campo é nulo.

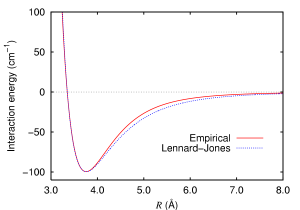
Aplicação interessante: O Potencial de Lennard-Jones.

Depois de tudo que vimos sobre energia potencial e potencial é hora de falarmos sobre uma aplicação interessante.

Em 1925 o físico J.E Lennard-Jones propõe uma função de energia potencial que inclui tanto forças atrativas quanto repulsivas entre dois átomos de uma molécula diatômica, por exemplo. Isso torna esse potencial particularmente interessante e de simples tratamento, podemos escrevê-lo da seguinte forma:

$V_{L.S}(r)=4\epsilon\left[\left(\frac{\sigma}{r}\right)^{12}-\left(\frac{\sigma}{r}\right)^{6}\right]$

Onde $\epsilon$ e $\sigma$ são constantes que podem ser ajustadas experimentalmente.

Comparação do potencial de Lennard-Jones, experimental e teórico.

A nossa primeira curiosidade nesse potencial é conhecer essas forças atrativas e repulsivas entre os dois átomos. Como vimos anteriormente à força se relaciona com o potencial da seguinte forma:

$F(r)=-\frac{dV}{dr}$ que também pode ser escrito em termos do gradiente: $F(r)=-\nabla V$

Realizando a derivada em $r$ temos então a força:

$F(r)= 4\epsilon\left[12\frac{\sigma^{12}}{r^{13}}-6\frac{\sigma^{6}}{r^7}\right]$

Agora temos uma curiosidade em particular, suponha que um dos átomos possua massa bem maior que a do outro átomo, e esse primeiro átomo permanece fixo enquanto o de menor massa oscila em torno de um ponto de equilíbrio entre eles, qual é esse ponto de equilíbrio e qual é a freqüência de vibração desse átomo de pequena massa?

Vimos anteriormente que o ponto de equilíbrio é o valor de $r$ em que $F=dV/dr=0$ e o período de oscilação é dado por:

$T=\frac{2\pi}{\omega_{0}}$

em que $\omega_{0}=\sqrt{\frac{K}{m}}$

Como o ponto de equilíbrio é aquele onde a força $F(r)$ é zero, temos:

$F(r)= 4\epsilon\left[12\frac{\sigma^{12}}{r^{13}}-6\frac{\sigma^{6}}{r^7}\right]=0$

Agora brincamos um pouco com a álgebra e obtemos:

$r= \left(2\right)^{1/6}\sigma$

Esse é o nosso ponto de equilíbrio no qual o átomo de menor massa oscila. Como o movimento é uma oscilação podemos encontrar uma constante restauradora $K$ a partir da derivada segunda do potencial:

$\frac{d^2V}{dr^2}=4\epsilon\left[156\frac{\sigma^{12}}{r^{14}}-42\frac{\sigma^{6}}{r^8}\right]\equiv K$

Uma vez que oscilação é em torno do ponto de equilíbrio, temos:

$\frac{d^{2} V}{dr^{2}}= 4 \epsilon \left[ 156 \frac{ \sigma^{12}}{\left( 2^{1/6}\sigma \right)^{14}} - 42 \frac{\sigma^{6}}{\left( 2^{1/6}\sigma\right)^{8}}\right]\equiv K$

Assim temos;

$K=68\frac{\epsilon}{\sqrt[3]{2}\sigma^{2}}$

Agora que temos $K$ podemos facilmente encontrar a período:

$T=2\pi\sqrt{\frac{m}{K}}$

Substituindo o valor de $K$ temos:

$T=2^{1/6}\pi\sigma\sqrt{\frac{m}{17\epsilon}}$

Agora que vimos essa interessante aplicação vamos para nosso ultimo tópico.

Teoremas de conservação.

– momento linear

Como vimos na equação (1.8) do primeiro texto, podemos ver que se a força resultante for zero teremos:

$\Delta p= 0$

Assim:

$p_{f}=p_{i}$

Fica evidente que o momento linear se conserva caso a resultante das forças externas sobre a partícula seja nula, e esse é nosso enunciado da lei de conservação do momento linear.

Trabalhando vetorialmente é interessante ressaltar que o momento linear pode ser conservado em uma determinada direção e não ser conservado em outra. Ou seja, se em uma determinada direção fixa $\vec{s}$ , tivermos $\vec{F} \hat{s}=0$ , então

$\frac{ d\vec{p}}{dt}\hat{s}=0$

então

$\vec{p} \hat{s}=cte$

Podemos enunciar então: a componente do momento linear se conserva na direção fixa em que a componente da força é nula.

– Momento angular

O momento angular de uma partícula de massa $m$ , com velocidade $v$ e localizada instantaneamente na posição $\vec{r}$ medida em relação a uma origem $O$ , é definida por:

$\vec{L}=\vec{r}\times\vec{p}$

Como você já deve ter notado, o momento angular é um análogo rotacional do momento linear. Derivando o momento angular temos:

$\frac{d\vec{L}}{dt}=\frac{d\left(\vec{r}\times\vec{p}\right)}{dt}$

$\dot{\vec{L}}=\dot{\vec{r}}\times\vec{p}+\vec{r}\times\dot{\vec{p}}$

em que $\dot{\vec{r}}\times\vec{p}=\vec{v}\times\left(m\vec{v}\right)=0$ uma vez que os vetores são paralelos, portanto:

$\dot{\vec{L}}=\vec{r}\times\dot{\vec{p}}$

Como $\dot{\vec{p}}=\vec{F}$ , então

$\dot{\vec{L}}=\vec{r}\times{\vec{F}}=\vec{N}$

Em que $\vec{N}$ é o torque em relação a mesma origem do momento angular, assim vemos que a variação temporal do momento angular de uma partícula é igual ao torque externo. Se o torque externo for igual a zero, $\vec{N}=0$ , o momento angular se conserva.

Da mesma forma que o momento linear pode se conservar em uma direção fixa e não em outra, o momento angular também pode se conservar para uma direção fixa $\vec{s}$ na qual $\vec{N}\hat{s}=0$ ;

$\dot{\vec{L}}\hat{s}=0$

$\frac{d}{dt}\left(\vec{L}{\hat{s}}\right)=0$

$\vec{L}{\hat{s}}=cte$

Assim a componente do momento angular é conservada na direção em que a componente do torque é nula durante o movimento.

Uma observação importante é que uma partícula pode ter momento angular em relação a uma origem, mesmo quando se translada em movimento retilíneo uniforme.

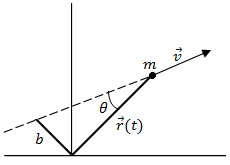
Partícula se movendo em MRU

O momento angular em relação à origem é dado por $\vec{L}=\vec{r}\times\vec{p}$ é um vetor em $-\hat{k}$ de magnitude $L=mrvsen\theta$ . Como a força resultante sobre a partícula é nula o torque também é nulo, o que mostra que o vetor momento angular é constante (em módulo e sentido), é fácil notar a constância do sentido, mas o da magnitude nem tanto. Observe que:

$L=mrvsen\theta =mvrsen\theta$

Em que $rsen\theta$ é a distância de máxima aproximação da partícula á origem, que é representada na figura por $a$ . Como essa distância é constante, o módulo de $\vec{L}$ também é constante, e com isso vemos a relação entre momento linear e angular em um movimento retilíneo, e com isso vemos a relação entre momento linear e angular em um movimento retilíneo.

Aqui encerro os tópicos introdutórios sobre mecânica clássica e espero que tenha sido útil para alguém. Qualquer dúvida, pedido, correção, sugestão será muito bem vinda e é só deixar nos comentários. Estou pensando em fazer talvez mais dois capítulos desses tópicos, um sobre forças centrais e outro sobre rotação de corpos rígidos, mas só farei se houver interesse por parte dos leitores.

[Thiago M. Guimarães]

Referências:

[1] Barcelos Neto. j: Mecânica Newtoniana, Lagrangiana e Hamiltoniana.

[2] Symons K.R: Mechanics vol 1

[3] Kazunori W.: Mecânica Clássica vol 1.

[4] Nussenzveig H.M: Física Básica Vol 1.

[5] Feynman R.P: Lectures on Physics Vol 1.

[6] Notas de Aula do Professor Canesin (UEM)

[7] Griffiths D. J.: Eletrodinâmica Vol.1

It is Relative, I Think!

Really, I think …

Arquivo mensal: fevereiro 2013

Tópicos Introdutórios de Mecânica Clássica – Parte 3